Difference between SNR and PSNR

In Image processing, we often use Signal to Noise Ratio (SNR) and Peak Signal to Noise Ratio (PSNR) for quality measurement. I understood that SNR is the ratio of signal power to the noise power. In terms of images, it shows how the original image is affected by the added noise. In PSNR, we take the square of the peak value in the image (in case of an 8 bit image, the peak value is 255) and divide it by the mean square error. The SNR and PSNR are used to measure the quality of an image after the reconstruction. I understand that higher the SNR or PSNR, the reconstruction is good. What I don't understand is how SNR and PSNR differs in terms of their conclusion about the reconstructed image. What the PSNR of an image concludes that the SNR of the same image can't conclude ? Simply how the conclusion of PSNR differs from the conclusion of SNR?  These are the questions I had when tried to completely understand what is this SNR and PSNR. If you too have the same questions, read further to get clarified. Let's start with the mathematical definitions. Discrete signal power is defined as Ps=∑−∞∞s2[n]=|s[n]|2. We can apply this notion to noise w on top of some signal to calculate Pw in the same way. The signal to noise ratio (SNR) is then simply PSNR=PsPw If we've received a noise corrupted signal x[n]=s[n]+w[n] then we compute the SNR as follows PSNR=PsPw=Ps|x[n]−s[n]|2. Here |x[n]−s[n]|2 is simply the squared error between original and corrupted signals. Note that if we scaled the definition of power by the number of points in the signal, this would have been the mean squared error (MSE) but since we're dealing with ratios of powers, the result stays the same. Let us now interpret this result. This is the ratio of the power of signal to the power of noise. Power is in some sense the squared norm of your signal. It shows how much squared deviation you have from zero on average. You should also note that we can extend this notion to images by simply summing twice of rows and columns of your image vector, or simply stretching your entire image into a single vector of pixels and apply the one-dimensional definition. You can see that no spacial information is encoded into the definition of power. Now let's look at peak signal to noise ratio. This definition is PPSNR=max(s2[n])MSE. If you stare at this for long enough you will realize that this definition is really the same as that of PSNR except that the numerator of the ratio is now the maximum squared intensity of the signal, not the average one. This makes this criterion less strict. You can see that PPSNR≤PSNR and that they will only be equal to each pother if your original clean signal is constant everywhere. Now, why does this definition make sense? It makes sense because the case of SNR we're looking at how strong the signal is to how strong the noise is. We assume that there are no special circumstances. In fact, this definition is adapted directly from the physical definition of electrical power. In case of PSNR, we're interested in signal peak because we can be interested in things like the bandwidth of the signal, or number of bits we need to represent it. This is much more content-specific than pure SNR and can find many reasonable applications, image compression being on of them. Here we're saying that what matters is how well high-intensity regions of the image come through the noise, and we're paying much less attention how we're performing under low intensity.

What is Time domain and Frequency domain?

Time/Frequency are interrelated parameter of a signal and both representations are two views of a same signal. Most of the time in practice, the signal measuring, is a function of time. That is TIME-DOMAIN. In other words, when we plot the signal one of the axes is time (independent variable), and the other (dependent variable) is usually the amplitude. When we plot time-domain signals, we obtain a time-amplitude representation of the signal. 

This representation is not always the best representation of the signal for most signal processing related applications. In many cases, the most distinguished information is hidden in the frequency content of the signal. The frequency SPECTRUM of a signal is basically the frequency components (spectral components) of that signal. The frequency spectrum of a signal shows what frequencies exist in the signal. The below represents a signal in time domain and frequency domain.

Demo :

Here the square like wave f is the time domain and it contains 6 different frequencies in it but we are unable to see this information when we are just looking at the TIME DOMAIN representation. So when we take fourier transform of the time domain signal, it reveals the number of frequency it has with amplitude of those frequencies.  This is said to be the Frequency Domain.

In the above demo :

Red Color --- TIME DOMAIN SIGNAL
Blue Color --- FREQUENCY DOMAIN SIGNAL

MATLAB Code:

clear all;
clc;
close all;
f=50;
 A=5;
Fs=f*100;
Ts=1/Fs;
t=0:Ts:10/f;
x=A*sin(2*pi*f*t);
x1=A*sin(2*pi*(f+50)*t);
x2=A*sin(2*pi*(f+250)*t);
x=x+x1+x2; % Creating Hybrid signal which will have more than 1 frequency.
plot(x)
F=fft(x);
figure
N=Fs/length(F);
baxis=(1:N:N*(length(x)/2-1));
plot(baxis,real(F(1:length(F)/2))) 

Ideal Low Pass Filter Concept in MATLAB

%IDEAL LOW-PASS FILTER

%Part 1
        
        f=imread(X);  % reading an image X

        P=input('Enter the cut-off frequency'); % 10, 20, 40 or 50.

        [M,N]=size(f); % Saving the the rows of X in M and columns in N
        F=fft2(double(f)); % Taking Fourier transform to the input image
%Part 2 % Finding the distance matrix D which is required to create the filter mask
        u=0:(M-1);
        v=0:(N-1);
        idx=find(u>M/2);
        u(idx)=u(idx)-M;
        idy=find(v>N/2);
        v(idy)=v(idy)-N;
        [V,U]=meshgrid(v,u);
        D=sqrt(U.^2+V.^2);

%Part 3
        H=double(D<=P); % Comparing with the cut-off frequency to create filter mask 
        G=H.*F;               % Multiplying the Fourier transformed image with H
        g=real(ifft2(double(G))); % Inverse Fourier transform
        imshow(f),figure,imshow(g,[ ]); % Displaying input and output image
        end

Demo:

Reading an image:

Taking fourier transform of the above image, we get:

 Based on the cut-off freq (P) we design the filter function H , Here the cut-off frequency is nothing but radius of the white circle in the below image. The below image is usually referred as filter mask.

 

Performing filtering by using G=H.*F;% Multiplying the Fourier transformed image with the filter mask H. Please note the convolution in time domain to equal to multiplication in frequency domain.

 To the filtered output, we take inverse fourier transform for the above image and we get:

 This is the Ideal Low pass filtered image. 

What is Digital Image Processing?

I will be using simple language to explain the concepts. To understand Digital Image Processing, let us see each word individually.

Image:

For standard definitions about image you can refer to the wikipedia page : Image Definition  . If you have any difficulty in understanding that definitions, here is my definition for the image.

"Image" is the visual representation of information. That's it. Short and simple. If you are a person who isn't sure what the word "information" means, read further. "Information" is description of something or anything. To understand what the "visual representation" means here, read the below example.

 I already told that "Information" is description of something. For example, my physical description is "Male, Young, Average height, Short hair, and Casually dressed". Here I have described my physical appearance in text, this is said to be representing an information through text. 

The same information if I had communicated to someone through my speech, it is said to be representing an information through audio. 

Similarly, the same information can be represented visually if I take a picture of myself and post it here.

The above image also conveys the same information i.e)  "Male, Young, Average height, Short hair, and Casually dressed" but it is represented visually. So we have now learned what is an image in an unconventional way.

Digital:

A digital image is a numeric representation of a two-dimensional image. It will have pixel values are numerical.

What is pixel ?

Pixel is a smallest sample in an image. To understand what is pixel, you must know how the images are captured digitally(without using film rolls). Watch the below video:

 Youtube Link: How to capture image digitally

I believe you have seen the above mentioned video. The smallest unit in the CMOS sensor is said to be the picture element. The term PIXEL is derived from this "PICture ELement". When the light reflected from the object that has to be captured hits this picture element in the CMOS sensor, the light energy is converted into electrical signals then this electrical signal converted into digital data (numerical value) using Analog to Digital Converter while saving to the memory card. So the image is now captured digitally.

 Processing:

Now that we have captured an image digitally. We to do perform some operation on the captured image to improve its perceived quality (It is said to be Image enhancement), reduce the size for storage and transmission (Image Compression) and etc.

Here is the block diagram for different processes that are done for digital images:


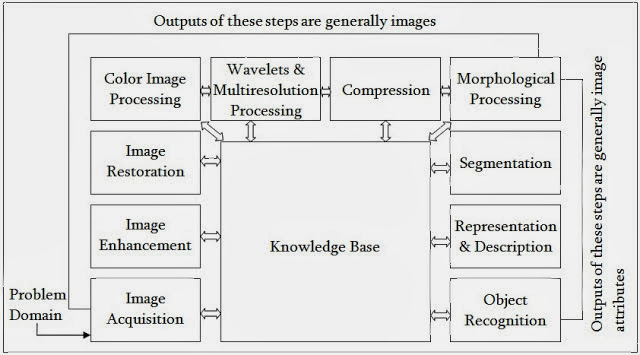
I hope this give you the basic understanding of Digital Image Processing.

Thirukural

Quote:

In sandy soil, when deep you delve, you reach the springs below;
The more you learn, the freer streams of wisdom flow.

Explanation:

Water will flow from a well in the sand in proportion to the depth to which it is dug, and knowledge will flow from a man in proportion to his learning.

 Quote:

So learn that you may full and faultless learning gain,
Then in obedience meet to lessons learnt remain.

Explanation:

Let a man learn thoroughly whatever he may learn, and let his conduct be worthy of his learning.